可靠性概论
只有在图纸设计阶段就考虑到使用场景时遇到的问题，再按图生产，才能制造出合格的产品。
1950年12月7日，美国电子设备可靠性专门委员会成立。
1952年8月21日，电子设备可靠性咨询组（AGREE）成立。
1953年，美国兰德公司给出衡量武器系统优劣的七项参数：性能、可靠性、精度、易损性、可操作性、维修性和可用性。
1957年6月，AGREE发表《军用电子设备可靠性》研究报告。
可靠性工程这门学科被认为是自1957年问世的。
1957年6月，AGREE发表的《军用电子设备可靠性》研究报告中，提出一套可靠性设计、试验及管理方法，形成了一套完善的可靠性设计、试验和管理标准。并在新一代产品的研制中，逐渐制定了较为完善的可靠性大纲，规定了定量的可靠性要求，进行了可靠性分配及预计、故障模式及影响分析（FMEA）和故障树分析（FTA），采用了冗余设计，开展了可靠性鉴定试验、验收试验和老炼试验，进行了可靠性评审等。
1970年代，可靠性发展步入成熟阶段。
1980年，美国国防部颁布《（D0DD 5000.40）可靠性及维修性》。
1985年，美国空军推行“可靠性及维修性2000年行动计划”（R&M2000），提出了“可靠性翻一番，维修性减半”的目标。
可靠性定义
可靠性 是指产品在 规定条件下 和
规定时间内 ，完成规定功能 的能力。
维修性 是指产品在 规定条件下 和
规定时间内 ，按规定的程序和方法维修时，保持或恢复到规定功能
的能力。
三个时间点
如果将产品比作人，那么产品从被研发、生产、出厂、使用到寿命终结的阶段，就好比人受精、怀胎、分娩、成长到死亡的阶段。将整个过程看做一个时间轴
$ t $ ， 那么其中的产品出厂（人的分娩）的时间就为 $ t=0
$，产品被研发和生产（人的受精、怀胎）的阶段，其时间被视为 \(t<0\) ，
产品被使用到寿命终结（人的成长到死亡）的阶段，其时间被视为 \(t>0\)
。这种方法是将产品简单划为三个时间点，例如在 \(t<0\)
时，研发和预制是两个不同的工作内容或阶段。
三个阶段
实际上，\(t=0\)
仅仅是个时间点，在可靠性研究过程中，产品寿命周期通常是按以下三个阶段进行研究：研发阶段 （\(t<0\) ）、生产制造阶段 （\(t<0\) ）和
使用至报废阶段 （\(t>0\) ）。
图1-1 质量与可靠性关系示意图
表 质量、可靠性与时间三者的关系
t = 0
使用产品合格率进行度量
t < 0
提高 制造过程
中的一致性和稳定性，以降低不合格率
t > 0
可靠性数学基础
所有可观测的现象包括 自然现象 和
社会现象 ，按照结果的确定性对此类现象进行分类可以分为：确定现象
和 不确定现象 。
graph LR
现象 --结果确定--> 确定现象
现象 --结果不确定--> 不确定现象 --具有统计规律--> 随机现象
不确定现象 --不具有统计规律--> 未知
随机
随机现象 具有统计规律性的 不确定现象 。
- 描述 过程/现象可能性
随机事件 随机现象的某种 可能结果 。
- 描述 结果可能性
随机试验 研究随机现象中各种 可能发生的结果的过程 。
- 描述 研究结果可能性的过程
随机现象之所以称之为随机现象，是因为现象发生后具有1个以上的可能结果，如果仅有1种结果，则可以称之现象和事件为
确定现象 和 确定事件 。
例如：
小球会落入某个洞口，小球的总数为2，小球落入洞口的现象是可观察可统计的，但小球确实地落在哪个洞口中具有不确定性，称之为现象。
但小球落入到洞口A或者洞口B，是可以预测到的结果，落入洞口A则称之为事件A，落入洞口B则称之为事件B，总称之为事件。
频率/概率
每一种随机现象的试验结果用 事件
一词来描述，则随机事件有可能在一次试验中可能发生，也可能不发生，其事件的发生可能性使用
频率 或 概率 来度量。
在相同试验条件下，进行 \(n\)
次试验，事件A的出现次数 \(m\) 称之为
频数 ，使用 试验总次数 \(n\) 和 事件A的频数 \(m\) 来表示 事件A在所有试验下的
频率 \(P^*(A)\) ：
\[
P^*(A)={m\over n} \tag{频率公式}
\]
频率 、频数 、频次
等术语在描述或者度量事件发生的可能性大小时，会因试验总次数太低 或
某个随机事件出现的次数具有波动性而导致不合理，就连以上三个词汇本身在描述时含有一定的随机性。
但在 大量重复
某一试验时，频率趋于稳定，此时该稳定值可以称之为随机事件的
概率 或 统计概率 ，使用 \(P(A)\) 表示。
即，概率 和 频率
两个词汇在描述随机试验中的事件时，最大的区别在于该事件频率值是否趋于
稳定 ，或者试验本身的总次数是否已经
足够大 。
数学符号 \(P^*(A)\) \(P(A)\)
特点 - 试验值 ，具有波动性近似反映
事件发生的可能性大小
- 理论值 ，由事件的本质属性决定精确反映 事件的可能性大小
概率分布
常用的分布函数由：两点分布、二项分布 、泊松分布 、均匀分布、正态分布 、对数正态分布 、指数分布
和 威布尔分布 等。
随机变量按照试验结果的值是否有限或连续可以分为：离散型随机变量
和
连续型随机变量 ，其中离散型随机变量在可靠性工程中常见的统计分布类型有
二项分布 和
泊松分布 ；连续型随机变量在可靠性工程中常见的统计分布类型有：
指数分布 、正态分布 、对数正态分布
和 威布尔分布 。
graph LR
id1[随机变量] --试验结果的值有限--> id2[离散型随机变量]
id1 --试验结果的值连续--> id3[连续型随机变量]
id2 --> 二项分布
id2 --> 泊松分布
id3 --> 正态分布
id3 --> 对数正态分布
id3 --> 指数分布
id3 --> 威布尔分布γ=0
可能取值范围 可能取值有限
给定区间（或无限区间）内可取得任意数值
可能取值符号 \(x_1,
x_2,x_3...x_n\) [0,∞)
概率函数 /分布律 某点的概率 \(P(X=x_i)=p_i,(i=1,2,3 ... n)\) /
概率密度函数 概率在点的变化率 /
\(f(x)=F'(x)={dF(x)\over dx}\)
概率分布函数 /累积概率函数 区间内的概率之和 \(F(x)=P(X≤x)=\sum_{x_k≤x}p_k\) \(F(x)=P(X≤x)\)
性质 - 任意取值变量的概率都在
[0,1) 之间：\(0≤P(X=x_i)=p_i＜1\) 1 ：\(\sum^n_{i=1}p_i=1\)
概率密度函数 或 概率分布
反映了随机变量的统计规律 。概率密度函数值反映了概率在该点的变化率，而非该点的概率。
以下需要区分几个概念，什么是
故障概率函数 、故障率函数 、故障概率密度函数 、故障密度函数 、可靠度函数 ？
故障概率函数 ，也称为 故障率函数 ，即
失败概率函数 ，用事件的失败概率进行求解。
故障概率密度函数 ，即适用于
连续型随机变量的故障概率函数。
在连续型统计分布中，故障密度函数 = 可靠度函数 * 故障率函数。
离散型随机变量分布
二项分布 \(P(x)=C^x_np^xq^{n-x}\) \(C^x_n = {n!\over x!(n-x)!}\) \(F(x)=\sum ^r_{x=0} C^x_n p^x
q^{n-x}\) \(C^x_n = {n!\over
x!(n-x)!}\) \(np\) \(npq\)
泊松分布 \(P(x)={(np)^x \over
x!}e^{-np}\) \(F(x) = \sum ^r_{x=0} {(np)^x \over
x!}e^{-np}\) \(\lambda\) \(\lambda = np\) \(\lambda\)
\(n\) 为
样本量，即抽取样本总数\(x\) 或 \(r\)
均为失败数，即抽取样本总数下失败的数量\(p\) 为 失败概率\(q\) 为 成功概率
需要注意 ： \(C^x_n =
{n!\over x!(n-x)!}\) ，是为
总试验次数的累乘 （阶乘）与
（成功次数的累乘 和 失败次数的累乘
之积） 的商。
二项分布
贝努力试验 ：随机变量的基本结果只有两种（成功/失败）的试验。
N重贝努力试验 ：随机现象是由N次相同的贝努力试验组成，每次试验结果
只有两种 且 互不影响 。
例题 2-1
某新产品在规定的生产条件下废品率为 0.2
，从批量较大的产品中随机抽取出 20 个，有 \(r\) （\(r=0,1,2...,10\) ）个废品的概率是多少？
解 ：已知某新产品的的废品与否，可以分为两种独立事件：成功
或
失败 （废品）。且单个产品是否成功或失败不影响下一个产品，即符合N重贝努力试验的要求。使用二项分布概率公式
\(P(x)=C^x_np^xq^{n-x}\)
代入，随机抽取的20个产品即为 \(n\)
，\(p\) 为失败的概率，即题目中的
0.2 或 20%，\(x\) 则为抽取总数 20
下的失败产品数量，代入可得： \[
P(X=r)=C^r_{20}0.2^r(1-0.2)^{20-r},r=0,1,2,3...10 \tag{例2-1}
\]
泊松分布
二项分布和泊松分布是不一样的。虽然都是离散型随机变量的分布类型，但是
二项分布适用于抽样总数小于 20 且 失败概率大于
0.05
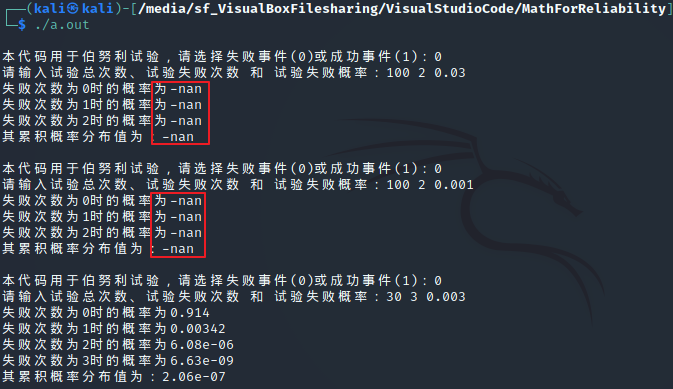
的情况 ，当抽样数无限大时，使用二项分布公式进行求解计算不了，代码中会出现
-nan
关键字，此时泊松分布可以轻松计算，因此，泊松分布被认为是二项分布在大抽样数下的扩展 。
反之，如果将适用于二项分布的数据代入泊松分布公式，虽然能够计算，但是可能会获得异常数据。
即，虽然人为泊松分布是二项分布的在大抽样数下的扩展，但是毕竟公式和理念都不一样，不能够用来互相验证。
image-20210902105513439
image-20210902105540683
例题 2-2
控制台指示灯平均失效率为每小时 0.001
次。如果指示灯的失效数不能超过 2 个，该控制台指示灯工作
500 小时的可靠度是多少？
解 ：结合上方题目和泊松分布的概率公式 \(P(x)={(np)^x \over x!}e^{-np}\)
可知，每小时平均失效率即为 失败概率 \(p\) ，工作时长500个小时即为抽样总数 \(n\) ，而失效灯数不能超过 2
个即为失败数 x ，代入公式可得： \[
P(x) = {(500·0.001)^x \over x!} ·e^{-500*0.001} = {0.5^x \over x!}
·e^{-0.5} \tag{例2-2 概率函数}
\] 然后求的其 \(P(0) + P(1)
+P(2)\) 之和： \[
F(2) = \sum^2_{0}P(x) = {0.5^0 \over 0!} ·e^{-0.5} + {0.5^1 \over 1!}
·e^{-0.5} +{0.5^2 \over 2!} ·e^{-0.5} = 1.625*0.606530 = 0.9856
\tag{例2-2 累积概率分布函数}
\]
连续型随机变量分布
正态分布
\(\frac{1}{\sigma\sqrt{2\pi}}e^{-{(x-\mu)^2}/{2\sigma^2}}\) \(\frac{1}{\sigma\sqrt{2\pi}}\int_x^\infin
e^{-{(x-\mu)^2}/{2\sigma^2}} dt\) \(e^{-(x-\mu)^2/(2\sigma)^2} / \int
^\infin _x e^{-(x-\mu)^2/(2\sigma)^2} dt\)
对数正态分布
\(\frac{1}{x\sigma\sqrt{2\pi}}e^{-(lnx-\mu)^2/2\sigma^2}\) \(\frac{1}{\sigma\sqrt{2\pi}}\int_x^\infin
\frac{1}{t}e^{-(lnt-\mu)^2/2\sigma^2} dt\) \(\frac{1}{x}e^{-(lnt-\mu)^2/(2\sigma)^2}/
\int_x^\infin \frac{1}{t}e^{-(lnt-\mu)^2/(2\sigma)^2} dt\)
指数分布
\(λe^{-λx}\) \(e^{-λx}\) \(λ\)
威布尔分布
$(){m-1}e {-(x/)^m} $
\(e^{-(x/\eta)^m}\) \(\frac{m}{\eta}(\frac{x}{\eta})^{m-1}\)
正态分布
在数学上，正态分布 （Normal Distribution）利用
均值 \(\mu\) 和
方差 \(\sigma^2\) 记为
\(\Nu(\mu, \sigma^2)\) 。
标准正态分布 ：正态分布曲线的 均值
为0，标准差 为1的正态分布，即 \(\mu = 0, \sigma = 1\) 。
一般正态分布 ：除标准正态分布以外的正态分布。任何正态分布都可以使用标准正态分布来计算。
一般正态分布
正态分布的密度函数 \(f(x)\) 为：
\[
\varphi(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-{(x-\mu)^2}/{2\sigma^2}}
\tag{正态密度函数}
\] 正态分布的可靠度函数 \(R(x)\)
为： \[
R(x) = \frac{1}{\sigma\sqrt{2\pi}}\int_x^\infin
e^{-{(x-\mu)^2}/{2\sigma^2}} dt \tag{正态可靠度函数}
\]
标准正态分布
标准正态分布以下简称标正，由于标正的均值为0，标准差为1，即 \(\mu = 0, \sigma = 1\) ，代入对应公式可得
标正密度函数 记为 \(\varphi(z)\)
，标正累积分布函数 记为 \(\Phi(z)\) ，分别如下： \[
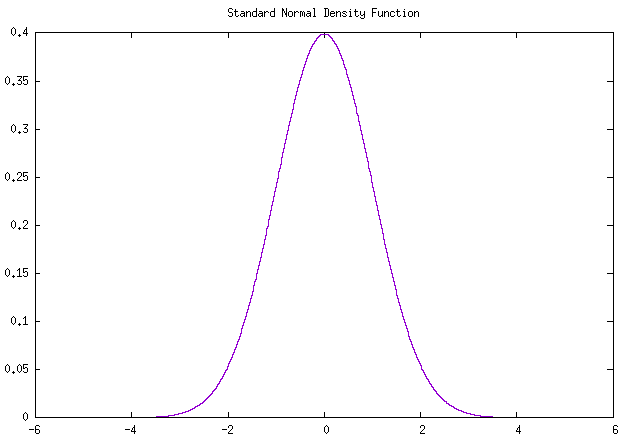
\varphi(z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2} \tag{标正密度函数}
\]
\[
\Phi(z) = \int^z_{-\infin} \varphi(z) \ dz = \frac{1}{\sqrt{2\pi}}
\int^z_{-\infin} e^{-z^2/2} \ dz \tag{标正累积分布函数}
\]
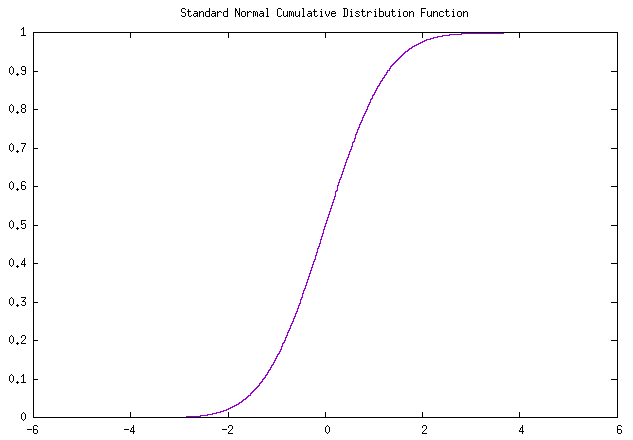
图 标准正态分布密度函数曲线 及 累积曲线
正态分布的 可靠度函数 为： \[
R(t) = 1-\Phi(\frac{t-\mu}{\sigma}) \tag{正态可靠度函数}
\]
image-20210903145950111
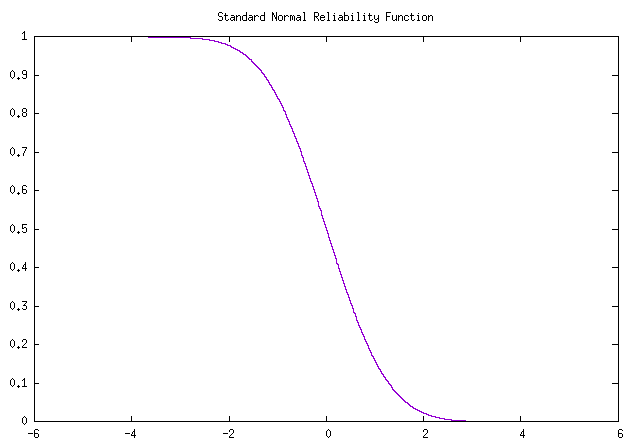
图 标准正态分布可靠度函数曲线
总结成下表：
一般正态 \(\varphi(x) =
\frac{1}{\sigma\sqrt{2\pi}}e^{-{(x-\mu)^2}/{2\sigma^2}}\) \(\Phi(x) = \frac{1}{\sigma\sqrt{2\pi}}
\int^x_{-\infin} e^{-{(x-\mu)^2}/{2\sigma^2}} \ dx\) \(R(x) =
\frac{1}{\sigma\sqrt{2\pi}}\int_x^\infin
e^{-{(x-\mu)^2}/{2\sigma^2}}\)
标准正态 \(\varphi(z) = \frac{1}{\sqrt{2\pi}}
e^{-z^2/2}\) \(\Phi(z) = \int^z_{-\infin} \varphi(z) \
dz = \frac{1}{\sqrt{2\pi}} \int^z_{-\infin} e^{-z^2/2}
\ dz\) \(R(t) =
1-\Phi(\frac{t-\mu}{\sigma})\)
正态分布的重要参数有以下几个：
工作时长 \(x\)
均值 \(\mu\)
标准差 \(\sigma\)
需要注意的是 ：
一般正态密度函数 的符号记为 \(f(x)\) ，标准正态密度函数
的符号记为小写的希腊字母 \(\varphi(z)\) 。一般其他分布的 累积分布函数 为 大写的 \(F(x)\) 。
标正累积分布函数 的符号记为大写的希腊字母 \(\Phi(z)\) ，与
标正密度函数
的符号发音一致，标正累积分布函数的值计算较为麻烦，可以通过查表获得 。就标正比较特殊，需要全部用希腊字母 。因为 标正累积分布函数 和
标正可靠度函数 的曲线互为水平翻转。
例题 2-3
假设发电机的寿命服从正态分布，其均值为300小时，标准差为40小时。试求当工作时间为250小时时，发电机的可靠度是多少？
解 ：已知均值 \(u =
300\) ，标准差 \(\sigma = 40\)
且 工作时长为 250
小时，可代入正态可靠度函数进行求解，如下： \[
R(t) = 1- \Phi(\frac{t-\mu}{\sigma}) = 1-\Phi(\frac{250-300}{40}) = 1 -
\Phi(-1.25) \tag{例2-3 正态分布可靠度函数}
\] 其中，\(\Phi(-1.25)\) 和
\(\Phi(1.25)\) 互补（和为
1），可以通过查询标准正态累积分布表 或使用
自行编写的函数进行计算，可得 \(\Phi(1.25) =
0.89\) ，则发电机的可靠度为: \[
R(250) = 1-(1-\Phi(1.25)) = 1 - (1-0.89) = 0.89 \tag{例2-3 可靠度计算}
\]
正态分布的特性
\(\Phi(x)\) 和 \(\Phi(-x)\) 为 互补关系 ，即
\(\Phi(x) + \Phi(-x) =1\) 在 标准正态分布 下，可靠度 和
累积分布值 互补为1， \(R(t) =
1-\Phi(t)\) ，在 一般正态分布 下，需要注意加入
均值 \(\mu\) 和
标准差 \(\sigma\)
。
正态分布的用途
在可靠性工程中，正态分布具有以下三种用途：
分析由于磨损发生故障的产品，如机械装置。
对制造的产品及其性能是否符合规范进行分析。
用于机械可靠性概率设计。
对数正态分布
对数正态分布 （Logarithmic Normal Distribution） 是
正态分布随机变量的 自然对数 \(y = ln(x)\) ，记为 \(LN(\mu, \sigma^2)\) 。
特点 ：使用 对数正态分布 的对数变换
可以使得较大的数缩小为较小的数，且越大的数缩小的越明显。好处是使得较为分散的数据通过对数变换后，可以相对地集中起来，所以常把
跨几个数量级的数据用对数正态分布区拟合 （如下方例题2-4）。
适用产品/场景 ：半导体器件
的可靠性分析、机械零件 的疲劳寿命分析 或 在
维修性分析 中对维修时间数据的分析。
对数正态分布的密度函数如下，需要注意，该函数的取值范围为 \([0,\infin)\) \[
f(x)=\frac{1}{x\sigma\sqrt{2\pi}}e^{-(lnx-\mu)^2/2\sigma^2}\tag{对数正态分布密度函数}
\]
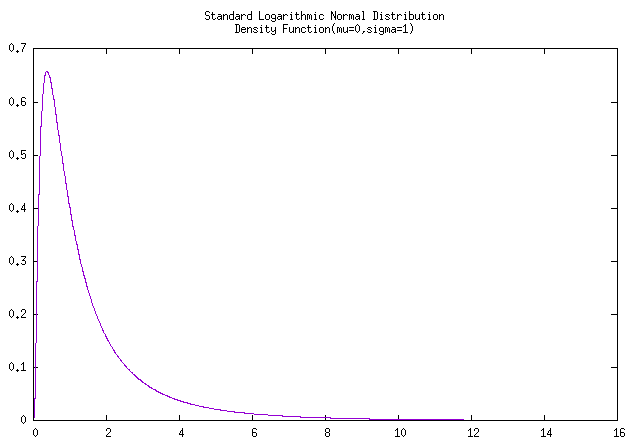
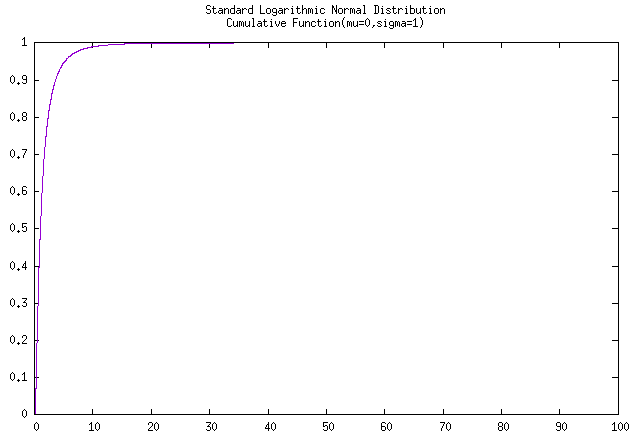
图 标准对数正态分布密度函数曲线 及 累积曲线
注意 ：应该是没有标准对数正态分布的吧，就代入 \(\mu = 0, \sigma = 1\) 进行计算求得图像
对数正态累积分布函数如下： \[
F(x) = \frac{1}{\sigma \sqrt{2\pi}} \int^x_0 \frac{1}{t}
e^{-{(lnt-\mu)^2}/{2\sigma^2}} \ dt \tag{对数正态累积分布函数}
\] 其可靠度函数如下： \[
R(x) = 1 - \Phi(\frac{ln(x)-\mu}{\sigma}) \tag{对数正态分布可靠度函数}
\] 其中，\(ln(x)\) 和 \(x\) 的均值和方差如下：
\(ln(x)\) \(\mu\) \(\sigma^2\)
\(x\) \(E(x)=exp(\mu +
\frac{\sigma^2}{2})\) \(Var(x)=exp(2\mu + \sigma^2) ·
[exp(\sigma^2)-1]\)
对数正态分布的重要参数有以下几个：
工作时长 \(x\)
均值 \(\mu\)
标准差 \(\sigma\)
例题 2-4
假设人们观察到炮管寿命服从对数正态分布，\(\mu = 9,\sigma = 2\) 。（注意，\(\mu\) 和 \(\sigma\) 是 \(ln(x)\)
的均值和标准差）求发射1000发炮弹时的可靠度。
解 ：
情况一 ：已知对数正态分布可靠度表格
在已知表格时，直接代入公式，然后查表计算即可。 \[
R(1000)=1-\Phi(\frac{ln1000-9}{2}) = 1-\Phi(-1.046) = 1-0.15 = 0.85
\tag{例2-4 可靠度计算}
\] 情况二 ：未知对数正态分布可靠度表格
在没有对数正态分布可靠度值表格可查询的情况下，是没有办法直接得出答案的。正常的思路如下：
将 \(\mu=9, \sigma=2\) 代入密度公式
\(f(x)\)
然后在区间 \((0,1000]\)
内进行积分，通过累计分布函数 \(\Phi(1000)\)
，可以得到其特定区间内的累积分布值。
然后使用 1 减去该累积分布值即可获得该可靠度值 \(R(1000)\) 。
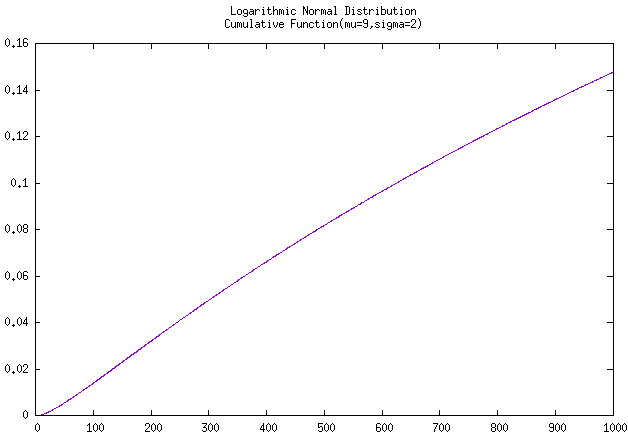
图 例题的对数正态累积分布曲线和可靠度曲线
上面两个图片是经由C++函数计算并使用gnuplot进行绘制的，实际计算得到本例题的
\(\Phi(1000) = 0.14781, R(1000)=
0.85219\)
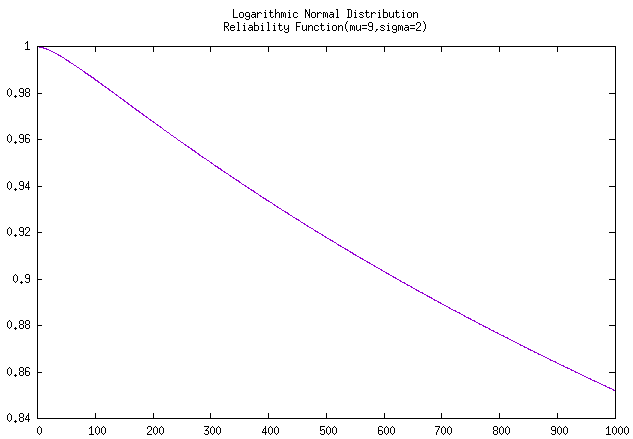
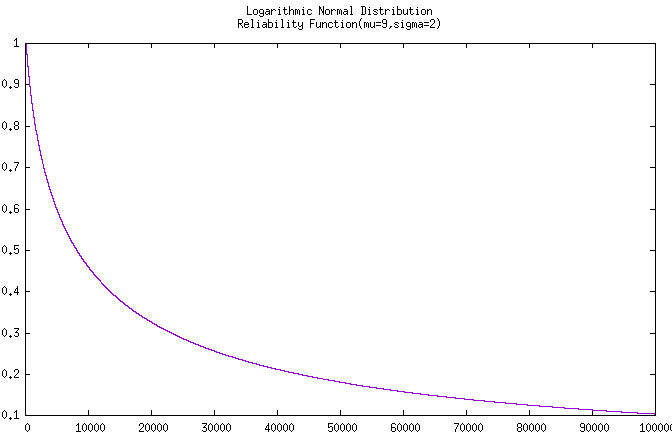
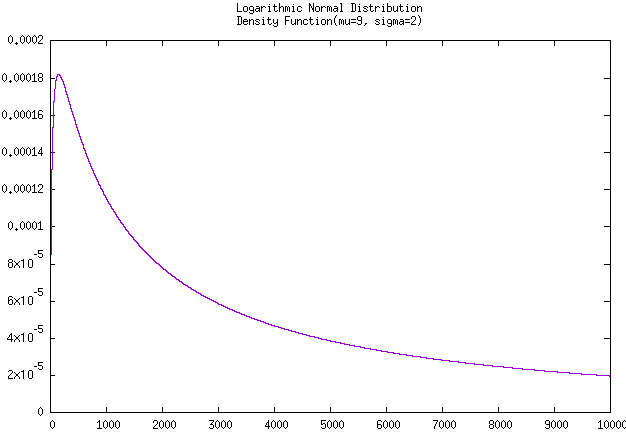
无聊着又稍微拟合了该产品在工作到 100,000 小时时的
可靠度曲线 和 工作到 10,000 小时时的
密度曲线 。
图 工作到10万小时的炮管的可靠度曲线 和 工作到1万小时的炮管的密度曲线
指数分布
指数分布 （Exponential Distribution）
是可靠性工程中最重要的一种分布。
当产品工作进入浴盆曲线的偶然故障期后，产品的故障率基本接近常数，其对应的故障分布函数就是指数分布。
优点 ：
参数估计简单容易，只有一个变量；
在数学上非常容易处理；
适用范围非常广；
大量指数分布的独立变量之和还是指数分布，具有可加性。
性质 ：
指数分布的失效率 \(\lambda\) 等于
常数 ；
指数分布的 平均寿命 \(\theta\) 和 失效率 \(\lambda\) 互为倒数，即 \(\theta = 1/\lambda\) ；
指数分布“无记忆性”。（无记忆性
是指故障分布为指数分布的系统的失效率，在任何时刻都与系统已工作过的时间长短没有关系。）
指数分布的密度函数如下： \[
f(x) = \left\{
\displaylines{\lambda e^{-\lambda x}, x ≥ 0\\ 0,x < 0}
\right. \tag{指数分布密度函数}
\] 其累积失效分布函数为： \[
F(x) = 1 - e^{-\lambda x} \tag{指数累积分布函数}
\] 其可靠度函数为： \[
R(x)=e^{-\lambda x} \tag{指数分布可靠度函数}
\]
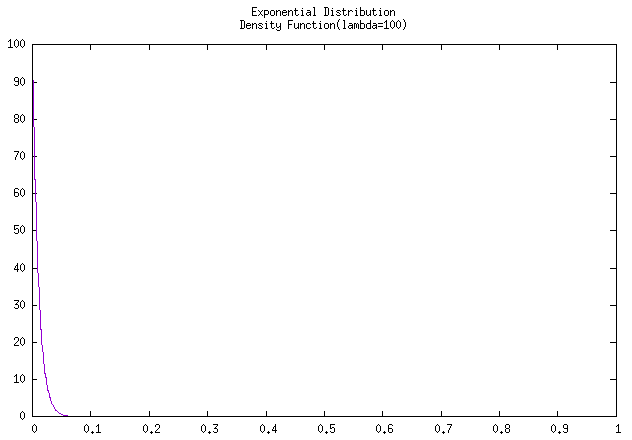
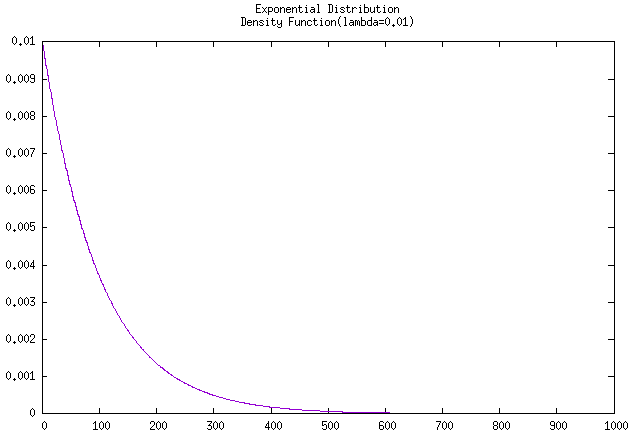
图 故障率为100 和 故障率为0.01的指数分布密度函数曲线
上图为错误例子啊，因为故障率 \(\lambda =
100\) 时已经高得离谱，且故障率和平均工作时长是呈反比的，故障率为
100 的话，就是说大概只能工作 0.01 小时（大概
36 s），所以会看到该 密度曲线
在x轴没到0.1就飞降。把故障率修改为
0.01，即大概能工作100个小时，就可以看到较为
正常
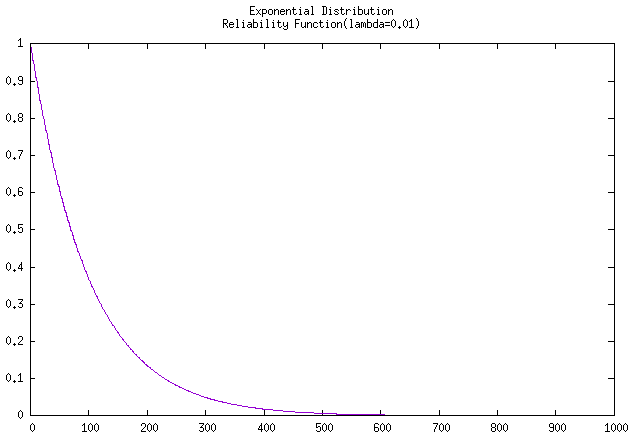
如果要求其可靠度曲线，则用 密度值 \(F(x)\) 除以 故障率 \(\lambda\) 即可，曲线如下：
image-20210903193144464
图 故障率为0.01的指数分布可靠度函数曲线
例题 2-5
机载火控系统的平均故障间隔时间是 100 小时，即 \(\theta = 100\)
小时，工作5小时不发生故障的概率是多少？
解 ：由题目已知 \(\theta =
100\) ， 即 \(\lambda = 0.01\)
，要求的是工作5小时不发生故障的概率，即求可靠度。
代入指数分布可靠度公式 \(R(x)=e^{-\lambda
x}\) 即可求得 0.951229，即 95.12%
。
威布尔分布
威布尔分布 （Weibull Distribution）是由
最弱环节模型 导出的，如链条的寿命就服从威布尔分布。
威布尔分布 是 通用分布
，通过调整分布参数可以构成各种不同的分布，可以为各种不同类型的产品的寿命特性建立模型。
威布尔分布既包括 故障率 为常数的模型，也包括故障率随时间变化的
递减 （早期故障）和
递增 （损耗故障）模型，因而可以描述更为复杂的失效过程。许多产品的故障率是单调递增的，威布尔分布可以很好地描述产品疲劳、磨损等损耗故障。
概率密度函数
\(f(t)=\frac{m}{\eta}(\frac{t}{\eta})^{m-1}exp[-(\frac{t}{\eta})^m]\) \(f(t)=\frac{m}{\eta}(\frac{t-\gamma}{\eta})^{m-1}exp[-(\frac{t-\gamma}{\eta})^m]\)
累积分布函数
\(F(t)=1-exp[-(\frac{t}{\eta})^m]\) \(F(t)=1-exp[-(\frac{t-\gamma}{\eta})^m]\)
可靠度函数
\(R(t)=exp[-(\frac{t}{\eta})^m]\) \(R(t)=exp[-(\frac{t-\gamma}{\eta})^m]\)
故障率函数
\(\lambda(t)=\frac{m}{\eta}(\frac{t}{\eta})^{m-1}\) \(\lambda(t)=\frac{m}{\eta}(\frac{t-\gamma}{\eta})^{m-1}\)
威布尔分布的重要参数有以下几个：
随机变量 \(t\) ，\(t≥0\) （两参数），\(t≥\gamma\) （三参数）
无量纲 形状参数 \(m,\ m>0\)
尺度参数 \(\eta,\ \eta>0\)
位置参数 \(\gamma, \
\gamma>0\)
除形状参数 \(m\)
以外，其他参数单位相同。
例题 2-6
人们发现某种特定的发射管的失效时间服从威布尔分布，其中 \(m=2, \eta = 1000\)
小时，试确定当任务时间为100小时时这种发射管的可靠度。
解 ：
威布尔分布除了时间 \(t\)
以外，就只剩下三个参数，而题目中并无使用位置参数 \(\gamma\)
，因此直接代入可靠度公式进行求解即可： \[
R(x) =exp[-(\frac{t-\gamma}{\eta})^m] = e^{-(t/\eta)^m} \tag{例2-6
可靠度求解}
\] 得到该产品在工作时长为100小时时的可靠度为： \[
R(100) = e^{-(100/1000)^2} = e^{-0.01} = 0.990049 ≈ 99\%
\]
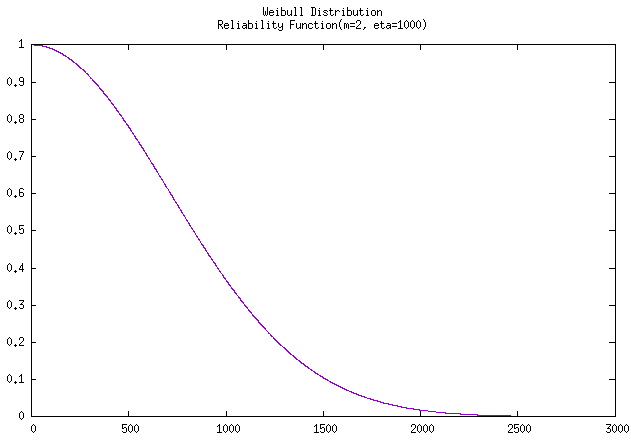
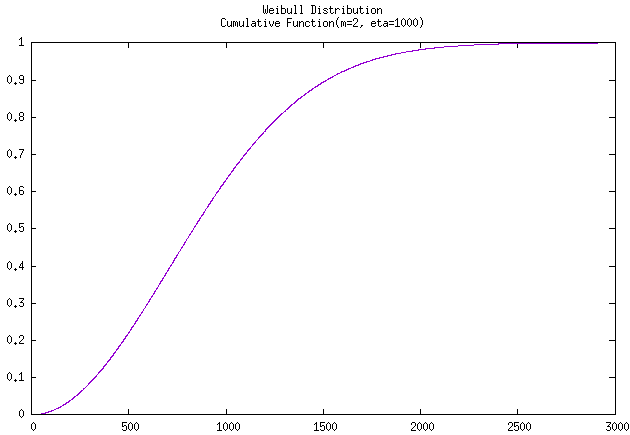
使用C++驱动GNUPLOT拟合该曲线至 \(t=3000\) 时的 可靠度曲线
和 累积曲线 如下：
图 例题2-6 威布尔分布的 可靠度曲线 和 累积曲线
参数估计
可靠性工程中，数理统计
是进行数据整理和分析的基础，其基本内容是统计推断 。
随机变量的概率分布虽然能很好地描述随机分布，但是通常不能对研究对象的总体都进行观测和试验 ，只能从中随机地抽取一部分子样进行观察和试验，获得必要的数据，对齐进行分析处理，然后对总体的
分布类型 和 参数 进行推断。
抽样相关概念
总体 ：也称为
母体 ，研究对象的全体。
个体 ：组成总体的每个基本单元。
样本 ：也称为
子样 ，在总体中随机抽取的部分个体。
样本值 ：在每次抽样后测得的具体数值（记为 \(x_1, x_2, x_3 ... x_n\) ）。
样本容量 ：样本所包含的个体数目（记为 \(n\) ）。
随机抽样 ：不掺入人为主观因素而具有随机性的抽样，即具有
代表性 和 独立性 的抽样。
样本统计量 ：是指子样 \(x_1, x_2, ..., x_n\) 是从母体 \(X\)
中随机抽取出来后，进一步提炼和加工后的统计量，如 均值
\(\overline x\) 、方差
\(S^2\) 、极差 \(R\)
子样之所以很宝贵，是因为包含了母体的各种信息，尚未对子样进一步提炼和加工处理前，母体的各种信息仍分散在子样中，子样经过加工成一些统计量之后可以反映出一些信息，如：均值
反映了母体数学期望信息，方差
反映了母体方差信息，极差
粗略地反映了母体分散程度，但不能直接用于估计母体的方差。下方为统计量的一些概念。
统计量相关概念
均值 ：反映了母体数学期望的信息，表示为 \(\overline x =\frac{1}{n}
\sum^n_{i=1}x_i\)
平均差 ：平均差是表示各个变量值之间差异程度的数值之一。指各个变量值同平均数的离差绝对值的算术平均数。
方差 ：方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，表示为
\(S^2=\frac{1}{n-1}\sum ^n_{i=1}(x_i-\overline
x)^2\) 。
标准差 ：是离均差平方的算术平均数的平方根，是方差的算术平方根，表示为
\(\sigma=\sqrt{S^2}\) 。
极差 ：极差又称范围误差或全距(Range)，以 \(R\)
表示，是用来表示统计资料中的变异量数(measures of
variation)，其最大值与最小值之间的差距，即最大值减最小值后所得之数据。是指一组数据内的最大值和最小值之间的差异，表示为
\(R=max(x_1,x_2, ..., x_n)-min(x1, x2, ...,
xn)\) 。
分布参数的点估计
如果 \(X\) 是一个具有概率分布 \(f(x)\) 的随机变量，样本容量为 \(n\) ，样本值为 \(x_1, x_2, ..., x_n\) ，则与其位置参数 \(\theta\) 相应的统计量 \(\hat{\theta }\) 的估计值。
此处，\(\hat{\theta}\)
是一个随机变量，因为它是样本数据的函数。在样本已经选好之后，就能得到一个确定的
\(\hat{\theta}\) 值，就是 \(\theta\) 的点估计。
点估计的解析法
在点估计的解析法中，有很多方法可以选择，如
矩法、最小二乘法、极大似然法、最好线性无偏估计、最好线性不变估计、简单线性无偏估计
和 不变估计。以上方法的特点如下：
矩法只适用于完全样本；
最好线性无偏估计 和 不变估计 已有国家标准《GB 2689.4-1981
寿命试验和加速寿命试验的最好线性无偏估计法（用于威布尔分布）》，但只适用于定数截尾情况，在一定样本量下有专用表格；
极大似然法和最小二乘法适用于所有情况，极大似然法是精度最好的方法。
极大似然法
极大似然估计（Maximum Likelihood Estimate,
MLE）是一种重要的估计方法，利用总体分布函数表达式及样本数据两种信息来建立似然函数。
特点 ：具有一致性、有效性 和 渐近无偏性
等优良性质。
缺点 ：求解方法最为复杂，需要用迭代法并借助计算机求解。
分布参数的区间估计
区间估计 ：在实际问题中，对于未知参数 \(\theta\) ，并不一定求出其点估计值 \(\hat{\theta}\)
为满足，仍希望求出其范围，并希望知道该范围包含未制参数 \(\theta\) 真值的置信概率的估计。
置信区间 ：表示计算估计的精确程度
置信度 ：是样品的试验结果在母体的概率分布参数（如均值或标准差）的某个区间内出现的概率，表示结果的可信性。
与置信度不同，可靠度 是指
样品在规定条件下和规定时间内正常工作的概率，反映的是产品本身的质量状况。
可靠性设计与分析
Gitee项目分享
适用于《可靠性工程师手册》的数学函数已经开源共享至Gitee，依托于
GNUPLOT 的图形绘制能力，可以轻松查看各种函数的曲线形状，十分方便。
Math-For-Reliability
在Gitee上的开源项目，开放给所有学习可靠性的人使用。
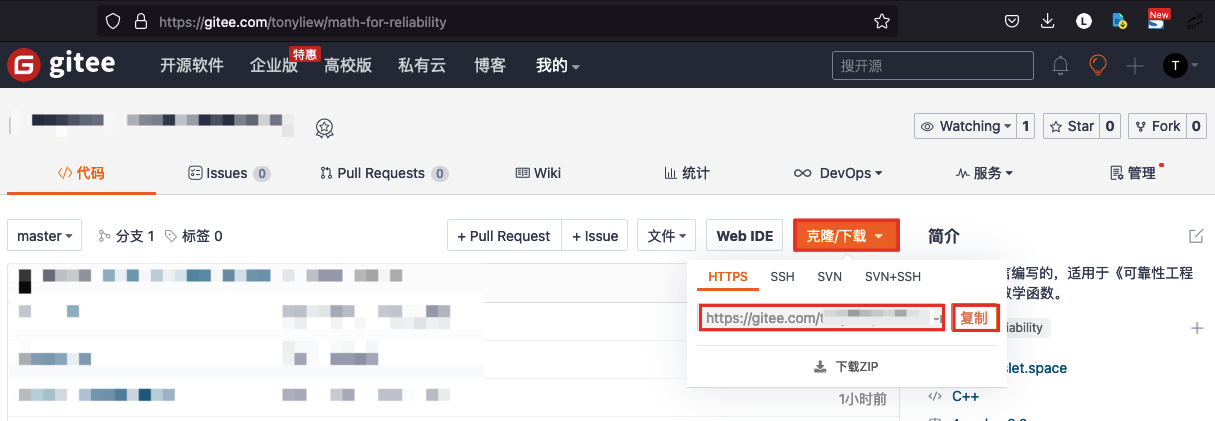
Gitee项目地址：https://gitee.com/tonyliew/math-for-reliability
DEBUG_RECORDS
20210902-01
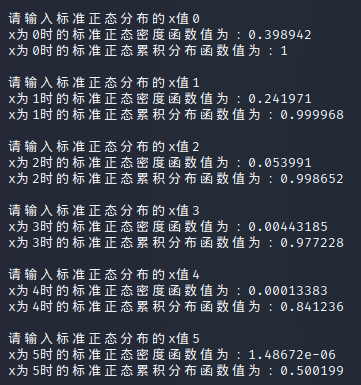
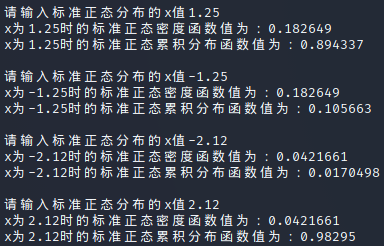
在Linux上运行标准正态累积分布计算函数，其计算结果与标准正态分布表方向相反了。\(x = 0\) 时的 \(\Phi(x)\) 值本应为0.5，结果和 \(x = 5\) 时的 \(\Phi(x)\) 值相反。
image-20210902193634846
一番检查发现积分函数可能不适用
image-20210902194119411
经过“校准”一番，终于修改好了，不知道还会不会卡Bug。
image-20210902194157770
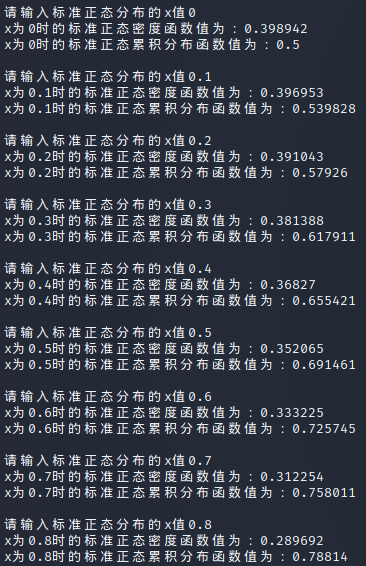
目前可以计算x值为正时的累积分布值，结果与标准正态分布表一致。
image-20210902194241093
重新解答完
2-3例题，发现知道了修改bug的方法，也只是补上了而已，哈哈哈哈。
image-20210902200537224
经过验证，结果正确。
image-20210902200910935
9月3日订正，为了生成标准正态累积分布的图形，发现带负号的
integral() 函数生成曲线时是 水平翻转
的。
图 标准正态分布的 累积（故障）函数曲线 和 可靠度函数曲线 互为水平翻转
仔细思考后发现，标准正态函数下，可靠度曲线值 是和
累积分布函数曲线 值各点互补为 1
的，很容易将累积分布函数和可靠度函数互相搞混，因此其图像才会互为
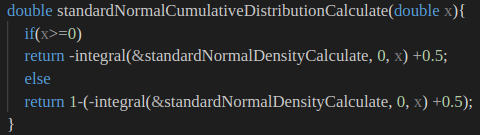
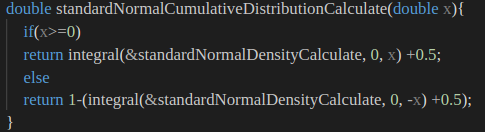
水平翻转 ，修改后的标正累积分布函数代码如下：
image-20210903144813581
参考
《可靠性工程师手册（第二版）》中国人名大学出版社 李良巧主编
概率分布函数、概率密度函数
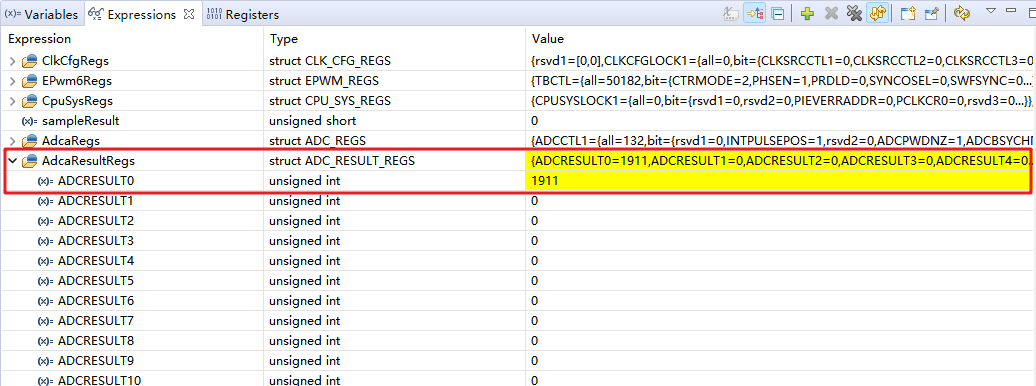
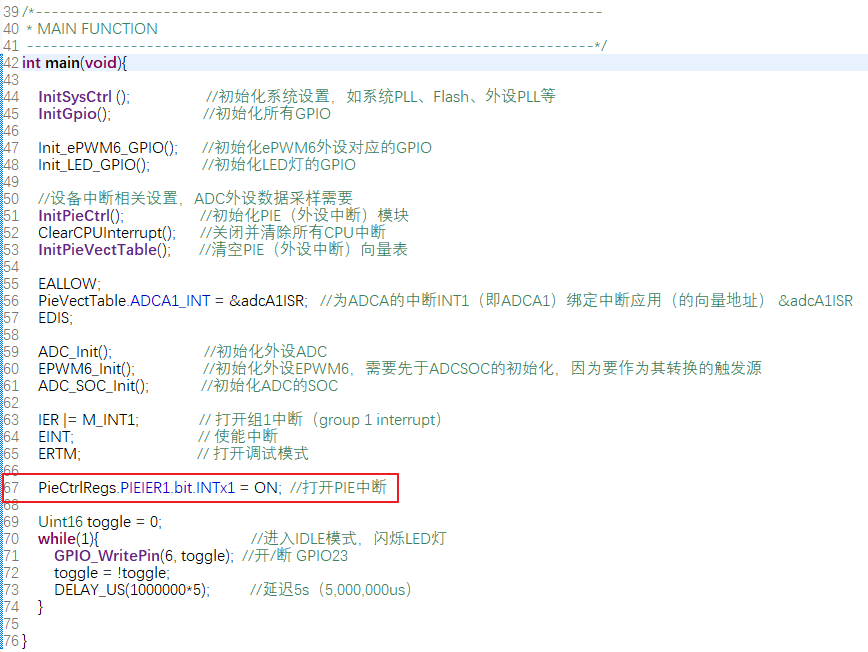
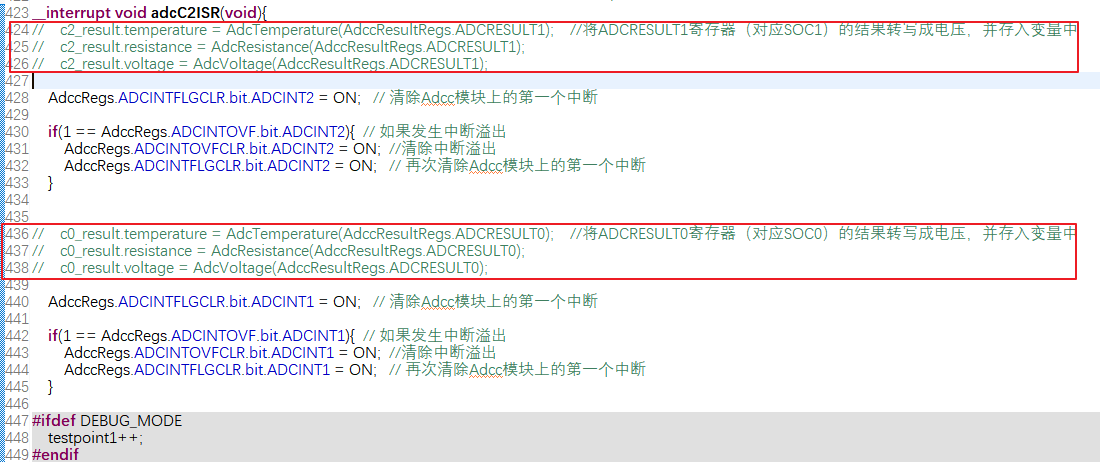
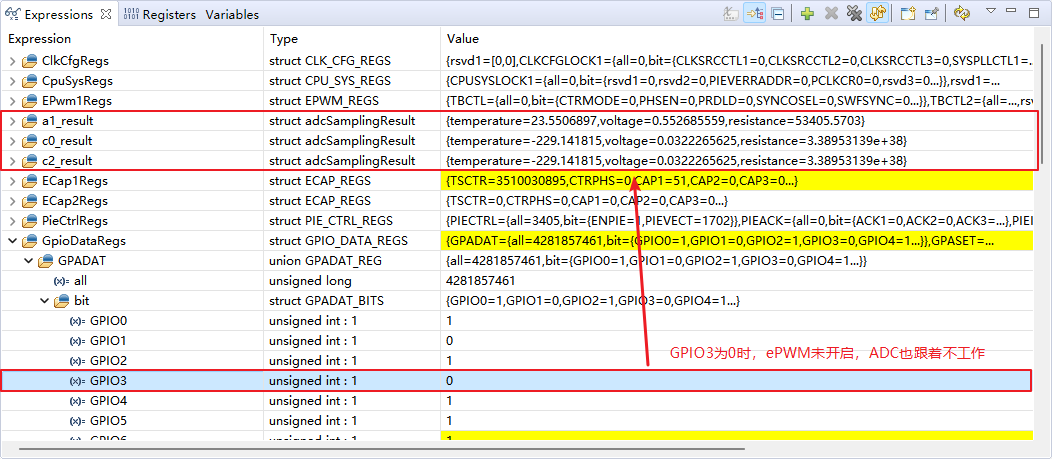
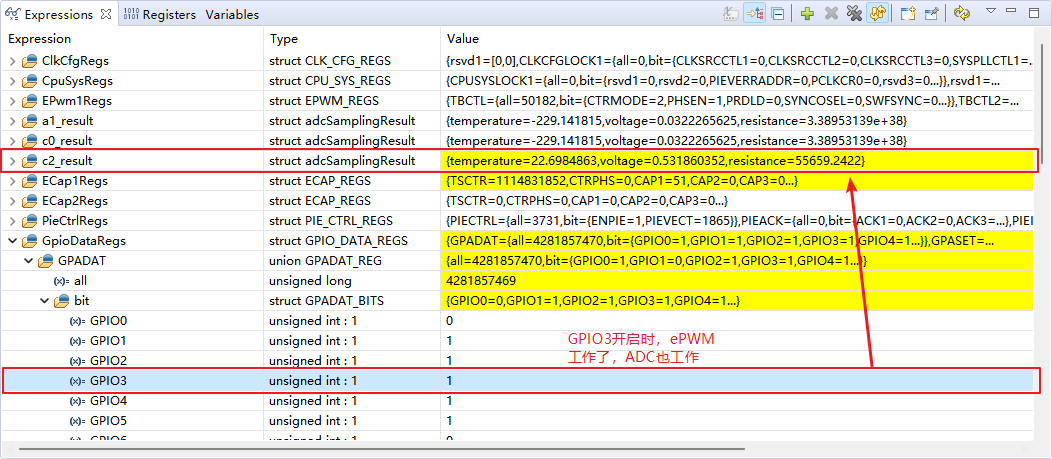
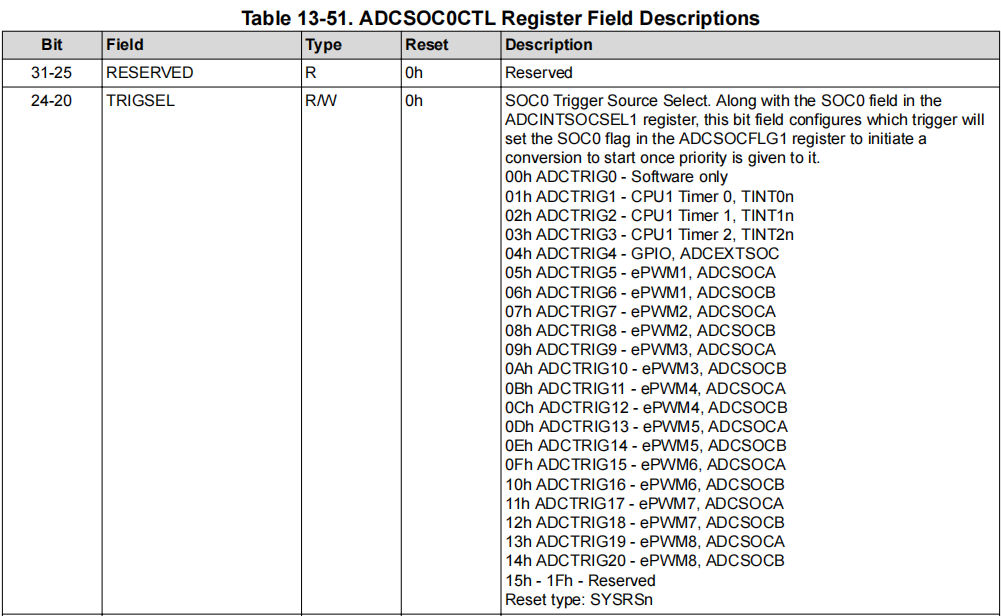
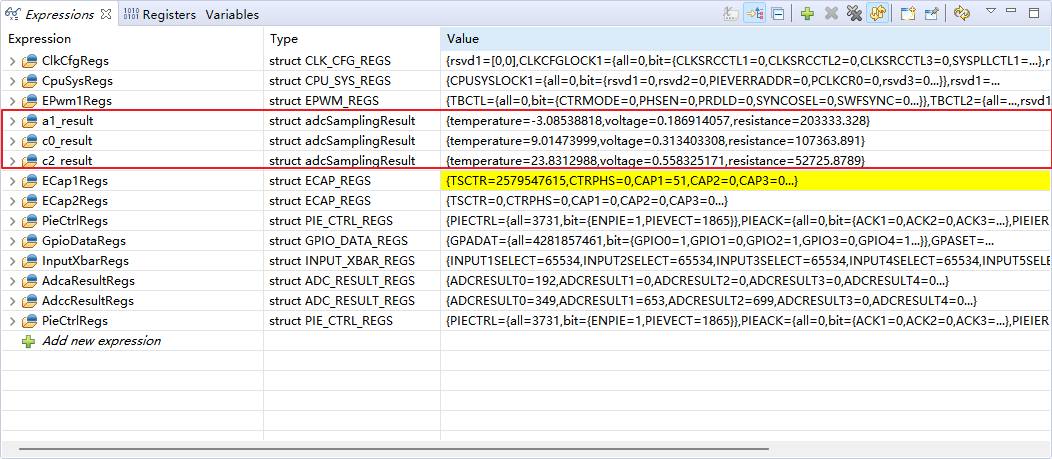
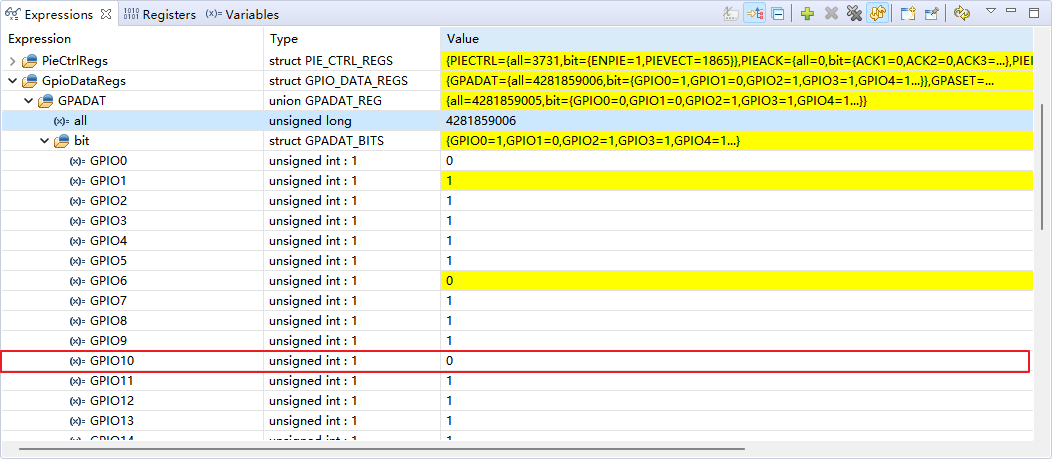
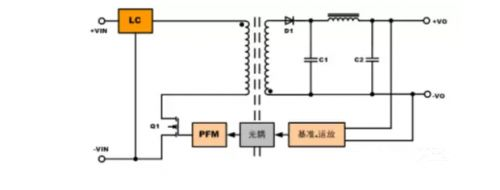
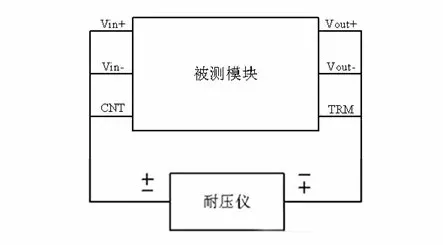
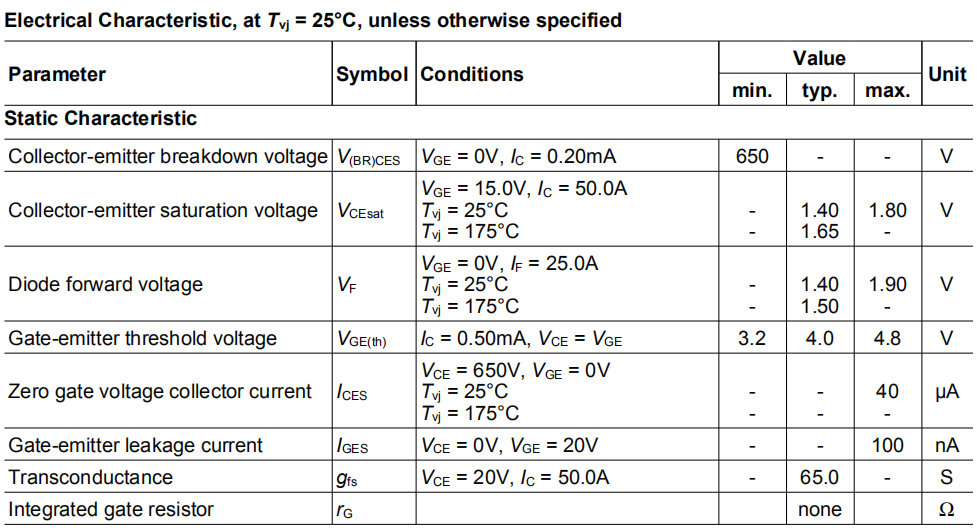
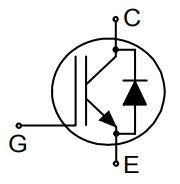
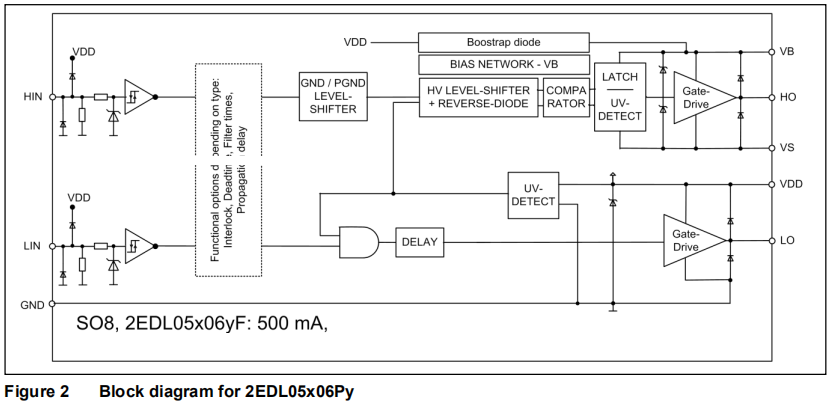
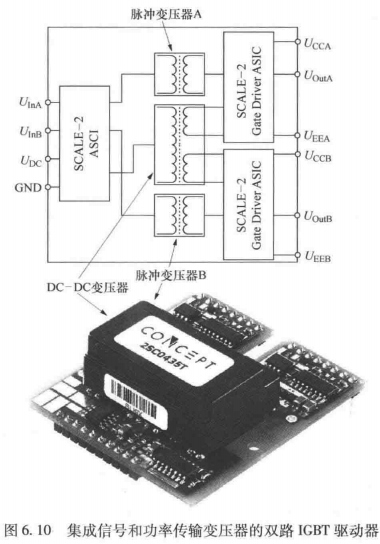
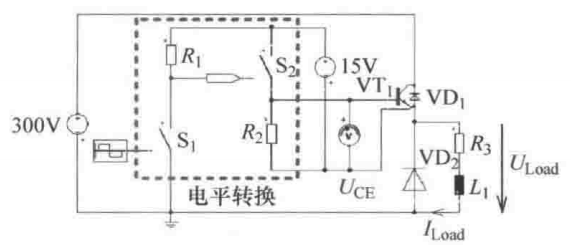
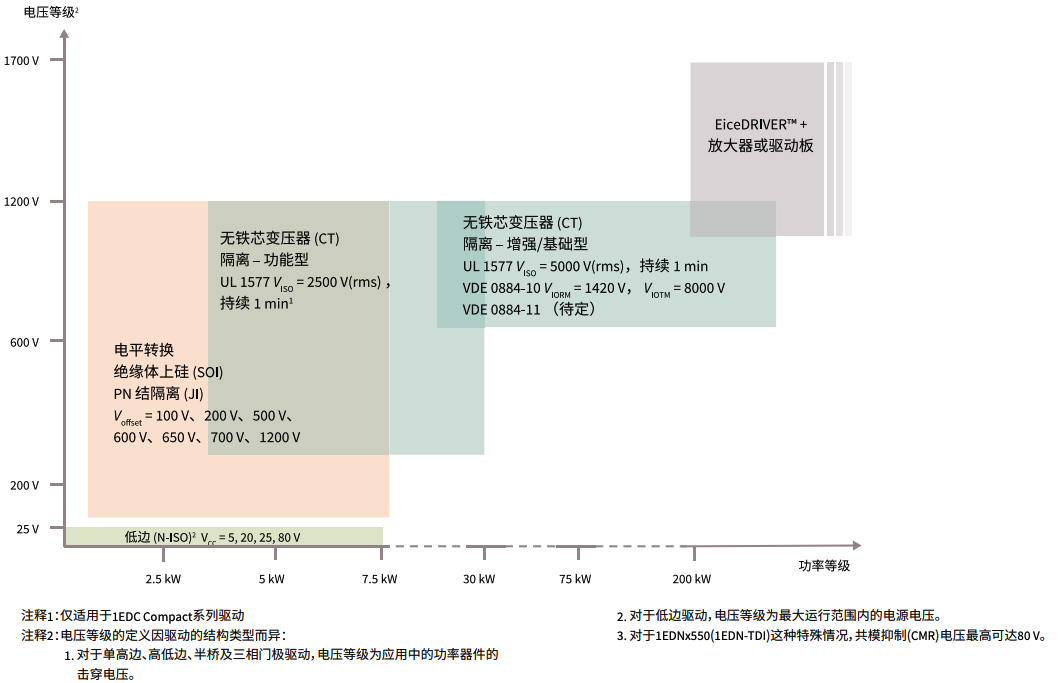
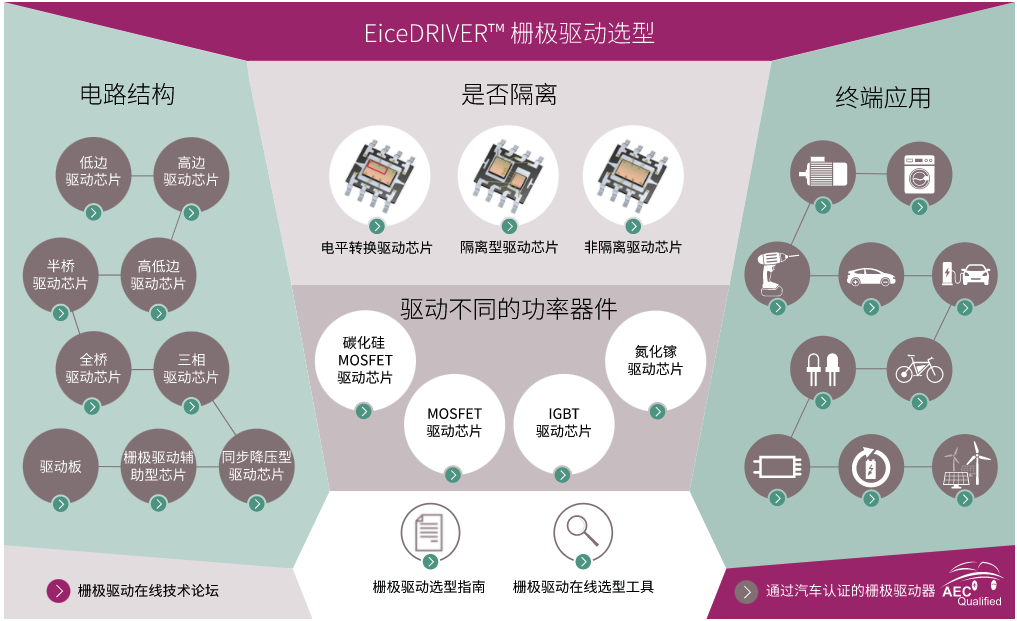
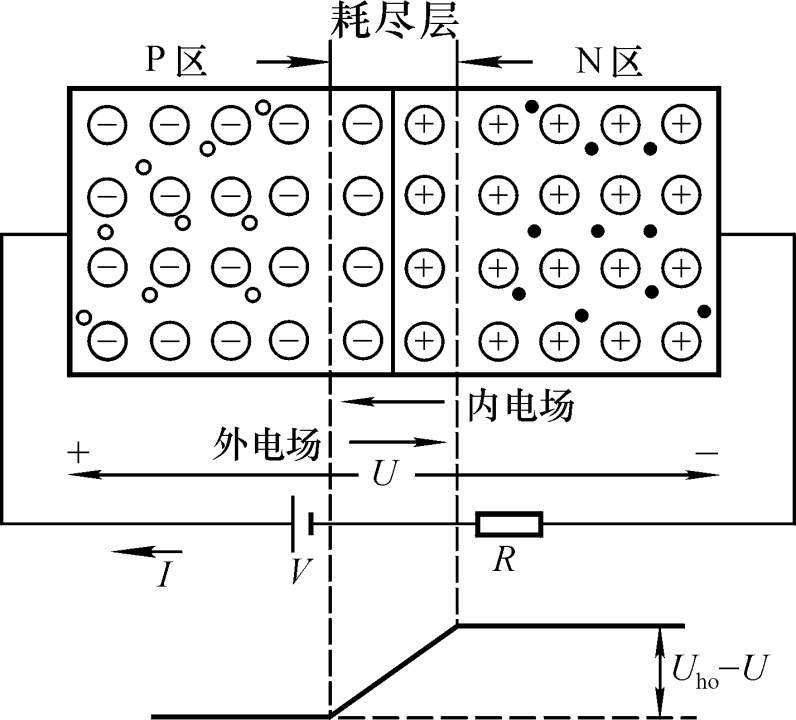
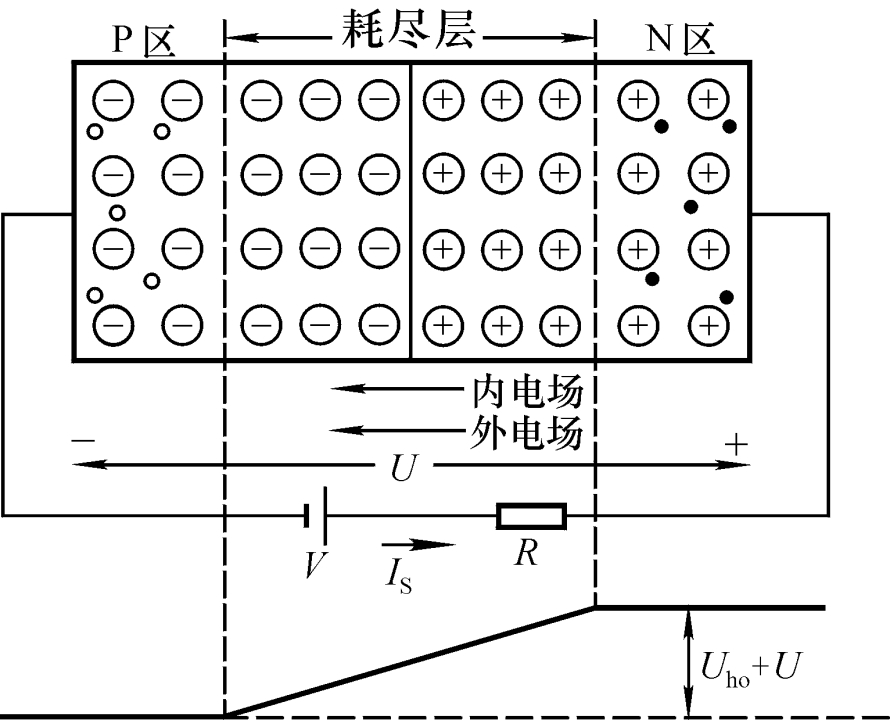
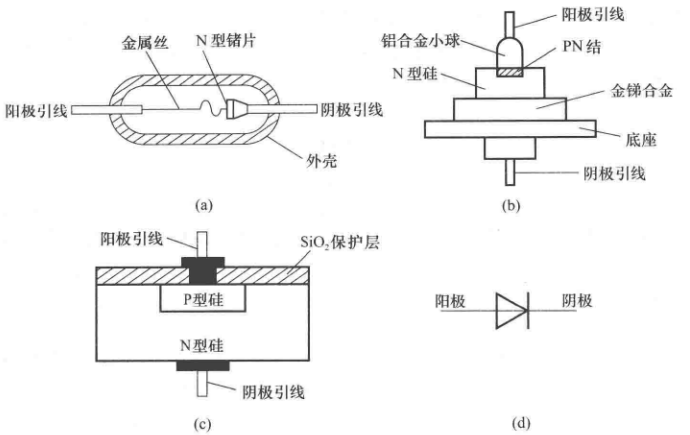
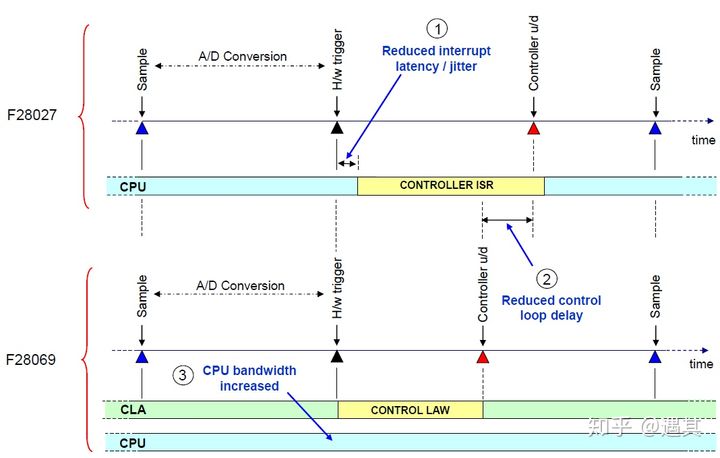
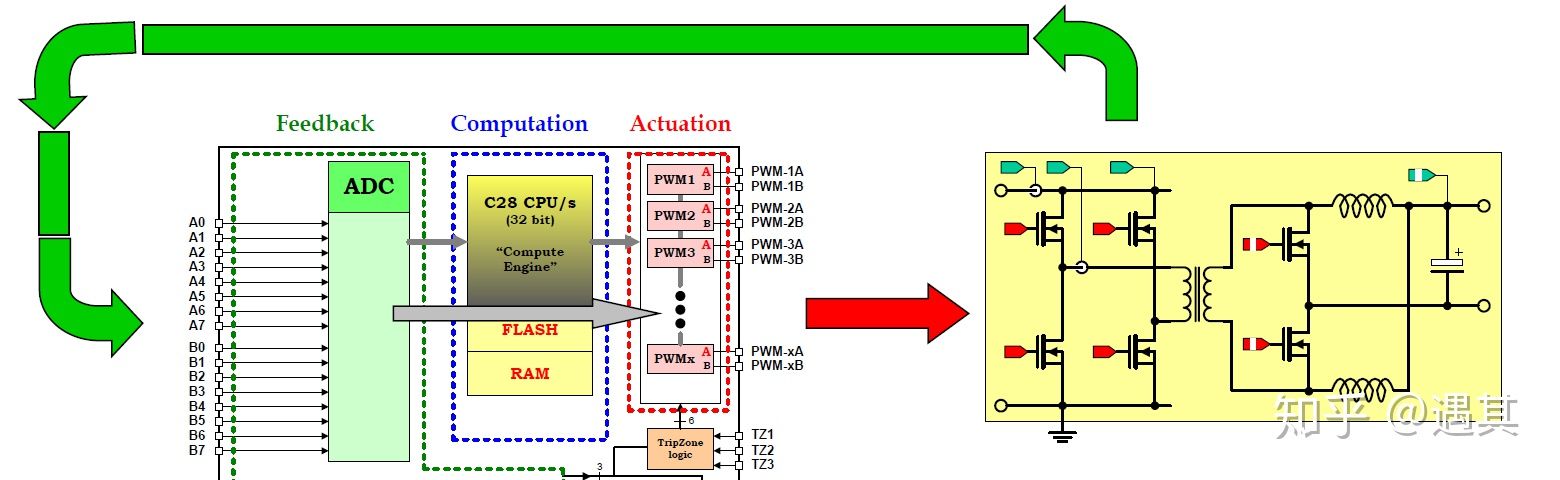闭环控制电路
